Drehmoment und Drehmomentschlüssel

[patapaya]

Ich glaub ich schnall's nicht.
Praxistest...

 

[jo.gi]

(...)
Anhängend nochmal an einem Beispiel visualisiert, mit stark vereinfachten Abmessungen.
(...)

Danke Dir für die Erklärung, auch wenn sie meine Vorstellung übersteigt. Nur Schulphysik halt.

Im Leben wäre ich nicht auf die Idee gekommen mit zwei Bezugsstellen zu rechen. Für mich ist die „halbe Hebellänge“ die Hälfte von der Strecke A-D (bezogen auf die Skizze in #56). Und das ist nicht Punkt C.
Für das „Knack“ hätte ich erwartet dass dies, wie auch immer, ausgelöst wird wenn bei B das eingestellte Moment über den Hebel B-A kleiner wird als das aufgebrachte Moment über den Hebel B-C, B-A, B-x … (Und das sind jetzt nicht die 100Nm)

Aber das soll jetzt keine wilde theoretische Diskussion auslösen. Wenn dies so gelehrt wird wird es schon einen Grund dafür geben.

 

[patapaya]

Wenn dies so gelehrt wird wird es schon einen Grund dafür geben.

Gelehrt wurde und wird vieles...
Und die Erde war ja auch mal eine Scheibe.
Ich versteh es einfach gerne - aber manchmal scheint es bei mir so weit nicht zu reichen.

 

[erik]

Das Moment wird tatsächlich nur zwischen dem Mittelpunkt des Vierkants und dem Knickpunkt zum Hebel ausgelöst. Wie weit weg man den Hebel hinter dem Knickpunkt anfasst, ändert dabei nur wie "leicht" es der Benutzer hat, den Drehmomentschlüssel zu bedienen.

 

[eisensturm]

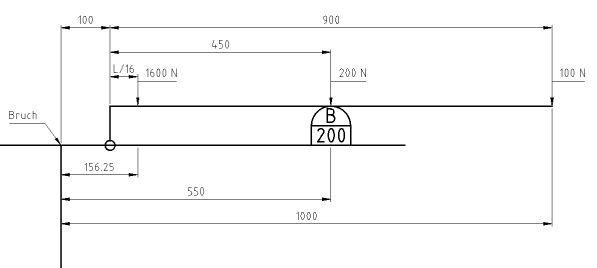
Habe das Bild nochmal ergänzt.

Der innere Hebel hat seinen Drehpunkt bei B.
In 450 mm Entfernung, an Punkt C, wird er vom Auslöser mit 200 N festgehalten. Das ist die gewünschte Einstellung an der Feder.
An Punkt B erreichen wir also immer genau 90 Nm, dann knickt der Schlüssel. Dabei ist es egal, wo man den Schlüssel (das Außenrohr) anfasst.
Beispiele
200 N (an Punkt C) x 0,45 m = 90 Nm
100 N (an Punkt D) x 0,9 m = 90 Nm

So lange der Knick nicht ausgelöst wurde haben wir einen starren Hebel.
An Punkt A wirkt also ganz direkt der ganze Hebel zwischen A und Angriffspunkt. A ist 100 mm von B entfernt.
Beispiele
200 N (an Punkt C) x 0,55 m = 110 Nm
100 N (an Punkt D) x 1 m = 100 Nm

 

[eisensturm]

Das Moment wird tatsächlich nur zwischen dem Mittelpunkt des Vierkants und dem Knickpunkt zum Hebel ausgelöst. Wie weit weg man den Hebel hinter dem Knickpunkt anfasst, ändert dabei nur wie "leicht" es der Benutzer hat, den Drehmomentschlüssel zu bedienen.

Das ist von der Bauart abhängig. Es gibt natürlich auch Schlüssel bei denen das zutrifft. Maßgeblich ist die Herstelleranleitung.
Im oben behandelten Fall trifft es nicht zu, deshalb der behandelte Fall.

 

[jo.gi]

(...)
So lange der Knick nicht ausgelöst wurde haben wir einen starren Hebel.
An Punkt A wirkt also ganz direkt der ganze Hebel zwischen A und Angriffspunkt. A ist 100 mm von B entfernt.
Beispiele
200 N (an Punkt C) x 0,55 m = 110 Nm
100 N (an Punkt D) x 1 m = 100 Nm

Soweit kann ich auch folgen.
Nur würde ich von dem Drehmomentschlüssel erwarten dass er bei etwa 180Nm an Punkt C knackt.
Wenn man dann trotzdem stumpf die 200Nm aufbringt ist es natürlich .

 

[René]

Nur würde ich von dem Drehmomentschlüssel erwarten dass er bei etwa 180Nm an Punkt C knackt.

Was er ja nicht kann, weil er anders geeicht ist.
Die Eichung kann halt immer nur für exakt eine Griffpisition stimmen.

 

[jo.gi]

Geeicht ist er auf das, was an Punkt A passieren soll.

Jetzt haben wir doch `ne theoretische Diskussion …
Angefangen hat das Ganze mit einem scherzhaft eingeworfenen „Halbe Länge = halbes Moment“.
Unterhalb der Auslöseschwelle ist der Drehmomentschlüssel ein starrer Hebel. Der Einfachheit halber mit dem einen Meter Länge aus der Skizze.
Hebelgesetz besagt: Halbe Länge = Doppelte Kraft.
Halbe Länge bei einem Meter liegt bei 0,5m. Dann passen auch die 200Nm als doppelte Kraft.
Bis hierhin einig?

Dann wird aus dem starren Hebel ein Drehmomentschlüssel und die doppelte Kraft wird auf einmal bei 0,55m aufgebracht. Warum? Logisch, dass dann ein höheres Drehmoment bei A anliegt, aber löst der Schlüssel auch dann erst aus?

Der Drehmomentschlüssel vergleicht an Punkt B irgendwas, nämlich das eingestellte gewünschte Drehmoment an Punkt A und der fixen Länge A-B mit dem, was auf der Seite B-D(C,x) aufgebracht wird. Also linke Seite von B zu rechter Seite auf der Skizze.
Knacken soll er, wenn „rechts“ größer wird als „links“.
Und nach meinem Schulphysik-Verständnis sollte es eigentlich egal sein wie „rechts“ mit Kraft x Weg aufgebracht wird.

Ich versteh es einfach gerne - aber manchmal scheint es bei mir so weit nicht zu reichen.

Ich bin wohl auch noch nicht soweit …

 

[René]

Ihr macht mich mit Euren Zweifeln an den Hebelgesetzen ganz meschugge. Also praktischer Test!

- 1/4"-DMS Proxon, eingestellt auf 15 Nm und während der messungen nicht verändert
- ANPUDS Drehmomentadapter 1,5 - 30 Nm, unterer 4-Kant fest im Schraubstock eingespannt.

3 Szenarien mit jeweils 3 Messungen:
- Krafteinwirkung ganz vorschriftsmäßig Handgriff, Auslösung bei 14,8 - 15,3 Nm
- aufgestecktes Rohr, Griffpunkt ca. 60 cm nach außen verschoben, Auslösung bei 13,4 - 13,8 Nm
- Griffpunkt auf ca. halber Länge des DMS (vor Beginn Plastikgriff), Auslösung bei 18,7 - 19,3 Nm

Dass die mit der Hand aufzubringende Kraft mit kürzerem Hebel zu und mit längerem abnimmt ist ja zumindest wenigstens klar, zumal ich auch keine Federwaage gehabt hätte.

Wer jetzt immer noch Zweifel hat, möge meinen Test bitte nachstellen.

 

[Sleipnir]

Wenn es zu physikalisch wird, da kann ich bei Diskussionen nicht mithalten :-)

Hier ein Beitrag aus dem Bauforum24:

Um diese Inhalte anzuzeigen, benötigen wir die Zustimmung zum Setzen von Drittanbieter-Cookies.
Für weitere Informationen siehe die Seite Verwendung von Cookies.

Drittanbieter-Cookies akzeptieren

Es gibt soweit ich weiß noch einen Weiteren, in dem gar gezeigt wird, dass man sogar bei mechanisch anzeigenden DMS, bei denen man den Mess-Drehpunkt am Vierkant intuitiv vermuten würde - den Griff genau in der Mitte anfassen sollte.

 

[René]

Genau solch ein Video hatte ich gestern schon gesucht, aber offenbar nur das vorherige Video, auf welches er sich hierin jetzt auch bezog, gefunden.

 

[eisensturm]

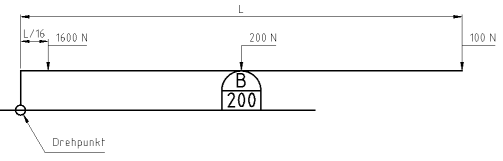
Jetzt mal Ruhe hier, hinsetzen, Hefte raus. Wir spielen Buzzer 200.


Für ein Quiz brauchen wir einen Buzzer. Da Kinder teilnehmen, brauchen wir den Buzzer 100, der aber ausverkauft ist. So nehmen wir den Buzzer 200.



Den können nicht alle Kinder drücken, also lassen wir uns etwas einfallen.



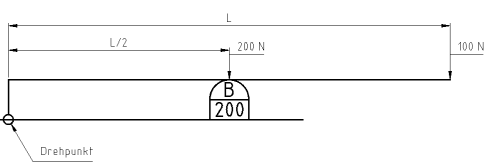
Keine Einwände, oder?

Fortsetzung folgt...

 

[eisensturm]

Der Quizmaster hat Verspätung, also werden die Kinder kreativ.

Wer ist am stäksten und kann den Buzzer am weitesten links des Hebels betätigen? Susi Ironbender schafft es bei L/8 und gewinnt.
Sie hat 800N aufgebracht, um den Buzzer 200 zu betätigen.



Einwände?
Fortsetzung folgt...

 

[eisensturm]

Jetzt kommt Kurt Felsenheber vom Klo und probiert es bei L/16.



jedoch

 

[eisensturm]

Bevor der Buzzer buzzt, bricht Omas alter Ausziehtisch ab.



Warum? Der Buzzer kann doch nur 200 N und jedes Mal vorher hat der Tisch gehalten.

 

[eisensturm]

Entscheidend war hier das Moment an der Bruchstelle.

1600 N x 0,15625 m = 250 Nm (wenn der Tisch gehalten hätte...)

Die Abmessungen kommen euch bekannt vor?

 

[eisensturm]

Aufmerksamkeitstest

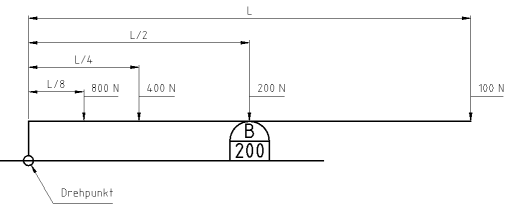
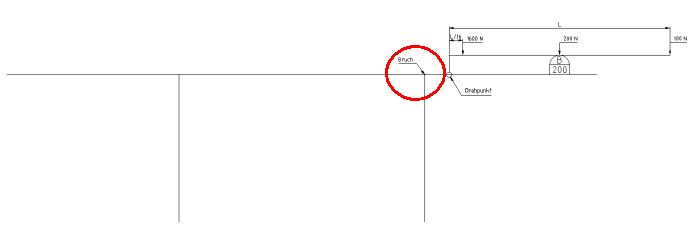
1) Welches Moment lag an der (späteren) Bruchstelle an, als Fred Federzweig den Buzzer 200 wie vorgesehen ganz rechts am Hebel (mit 100 N) betätigt hat?

2) Welches Moment lag an der (späteren) Bruchstelle an, als Susi Ironbender den Buzzer 200 bei L/8 (mit 800 N) betätigte.

 

[René]

1) 100 N * 1m = 100 Nm

2) 800 N * (0,9/8 + 0,1) m= 800 N * 0,2125 Nm = 170 Nm

3) 1600 N * (0,9/16 + 0,1)m = 1600 N * 0,15625 m = 250 Nm

 

[eisensturm]

Jawoll. Darfst heute eher nach Hause.

Die Anderen sind soweit?

So sähe das ganze Grafisch aus. Blau ist Kurt, grün ist Susi.



Angriffspunkt bei 100 mm bewirkt unendliches Drehmoment, weil genau am Drehpunkt des Auslösehebels.